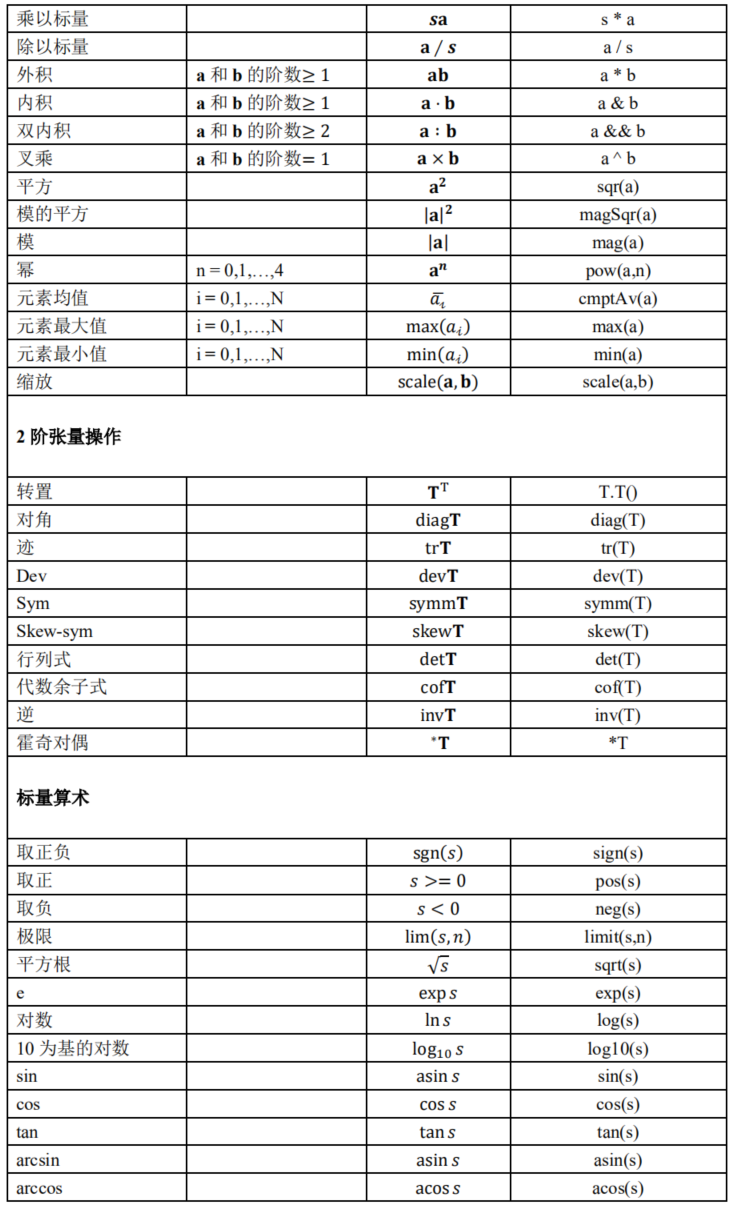
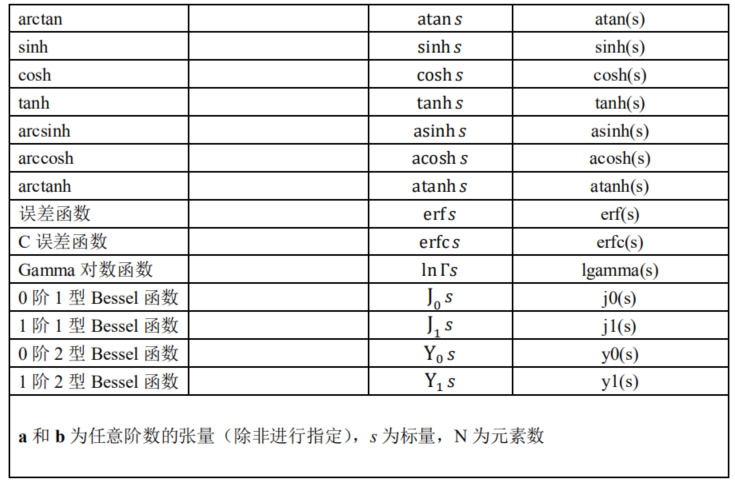
提取涡量的方法
参考文献 [1] :http://xiaopingqiu.github.io/2016/05/22/QAndLambda/
(1). 用流线去封闭涡
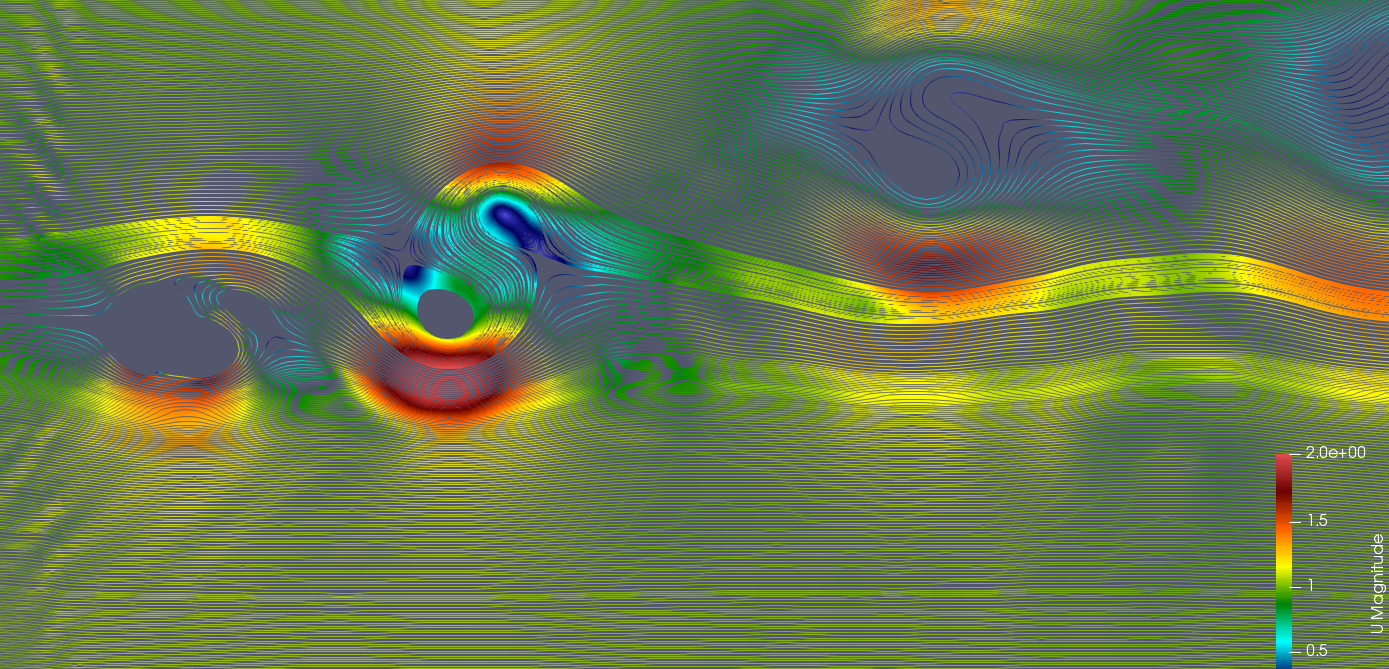
(2). 速度梯度 ∇U 的二阶不变量 Q 的定义为
$Q=\frac{1}{2}\left(|\mathbf{W}|^{2}-|\mathbf{S}|^{2}\right)$
$\mathbf{W}=\frac{1}{2}\left(\nabla \mathbf{U}-(\nabla \mathbf{U})^{\mathrm{T}}\right)$
$|\mathbf{W}|=(\mathbf{W}: \mathbf{W})^{1 / 2}$
$\mathbf{S}=\frac{1}{2}\left(\nabla \mathbf{U}+(\nabla \mathbf{U})^{\mathrm{T}}\right)$
$|\mathbf{S}|=(\mathbf{S}: \mathbf{S})^{1 / 2}$
OpenFOAM 中 Q 的计算用的是下面的方法
volTensorField gradU(fvc::grad(U));
volScalarField Q
(
IOobject
(
"Q",
runTime.timeName(),
mesh,
IOobject::NO_READ,
IOobject::AUTO_WRITE
),
0.5*(sqr(tr(gradU)) - tr(((gradU)&(gradU))))
);取Q>0的等值面
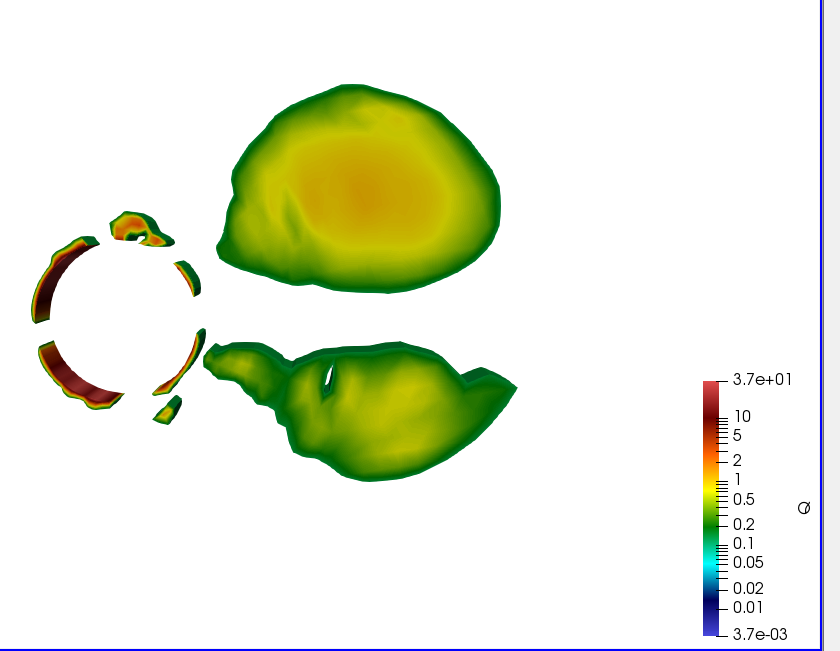
说到这里把张量运算符在of中的操作做一下总结
参考文献:[2] :《OpenFoam编程指南》.李东岳